O Efeito Dzhanibekov

Hoje, algo do campo da física para o curioso: o Efeito Dzhanibekov, também conhecido como teorema da raquete de tênis, explica uma instabilidade de corpos giratórios com três diferentes momentos de inércia. O momento de inércia indica a resistência de um corpo às mudanças em seu movimento rotacional. Depende do eixo de rotação específico e da geometria. Compreender a dinâmica dos sistemas hamiltonianos clássicos ainda é um objetivo crucial com uma infinidade de aplicações que vão muito além de sua descrição matemática. No caso de sistemas integráveis ​​com poucos graus de liberdade, uma abordagem eficiente é baseada em uma análise geométrica para caracterizar as propriedades dinâmicas do sistema mecânico. Tais fenômenos geométricos são tipicamente a origem da robustez de certos efeitos que podem ser observados experimentalmente. um deles é o chamado Efeito Dzhanibekov ou também chamado de efeito raquete de tênis.

Efeito Dschanibekow na leveza da ISS

Uma derivação teórica excelente e detalhada do fenômeno pode ser encontrada aqui (https://arxiv.org/pdf/1606.08237.pdf). Estamos lidando aqui com alguém que é um pouco mais rude, mas mesmo assim explica o fenômeno. Infelizmente, algum conhecimento prévio da dinâmica de corpos rígidos é necessário aqui:

Considere uma matriz de inércia (diagonalizada) com momentos de inércia I1 e I2 e I3 tais que I1 é o menor e I3 é o maior. Agora considere o movimento em torno do eixo do momento de inércia principal I3. O vetor de velocidade angular é:

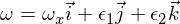
onde os épsilons são pequenas perturbações nos outros dois eixos principais. Se você inserir isso nas equações de Euler, obterá:

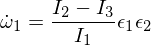
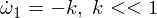
Agora diferenciamos a segunda equação de Euler:

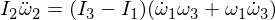
A substituição de ômega 1 e ômega 3 em nossa expressão e, uma vez que a multiplicação dos ípsilons os torna pequenos o suficiente para serem ignorados,

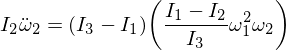
Isso nos dá uma equação diferencial para Omega 2 da forma:

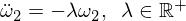
A solução básica é:

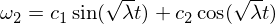
Daí sabemos que o distúrbio rotacional no eixo ômega-1 é estável e faz movimentos periódicos, ou na terminologia do movimento do corpo rígido, que faz uma precessão. O transtorno ômega 3 segue um argumento semelhante ao anterior, e vou deixá-lo como um exercício para você trabalhar com ele. Para o eixo intermediário, temos:

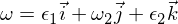
Inserido nas equações de Euler:

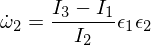
Diferenciar a terceira equação de Euler dá:

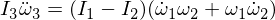
Vamos substituir nossas expressões derivadas:

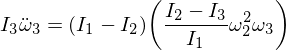
Agora reorganize e deduza a seguinte equação diferencial:

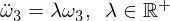
Observe que o coeficiente agora é positivo, o que, portanto, leva a soluções exponenciais:

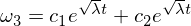
Esta solução mostra que o ômega 3 é instável com um distúrbio do ômega 2 ao longo do eixo intermediário!

O que isso significa?

Agora podemos combinar tudo o que derivamos e aprendemos para entender o teorema. Simplificando, se a rotação ao longo do eixo intermediário é perturbada, o resultado é uma equação diferencial com soluções exponenciais. Isso leva a um movimento instável, em contraste com o movimento preciso observado nos outros dois eixos. Este resultado é bastante surpreendente. Não há suporte intuitivo para tal teorema, pois não podemos imaginar por que o momento intermediário de inércia resultaria em uma rotação instável. Parece que é de natureza puramente matemática.